In che modo le imprese scelgono la combinazione ottima dei fattori produttivi?
In altre parole, come scelgono quale quantità di lavoro e di capitale impiegare per raggiungere un determinato livello di produzione minimizzando i costi?
Come vedremo, questo dipende dalla funzione di costo di lungo periodo e dalla funzione di produzione di lungo periodo dell’impresa.
Per comprendere appieno questi argomenti, bisogna conoscere i costi e la produzione in microeconomia. Ne abbiamo parlato approfonditamente in due post dedicati, che potete trovare cliccando sui pulsanti qui sotto:
In questo post anzitutto faremo una breve premessa sui costi e sulla produzione di lungo periodo (è solo una premessa perché questi sono trattati approfonditamente nei post accessibili attraverso i pulsanti qui sopra).
Richiameremo i concetti di isoquanto di produzione e di isocosto.
Successivamente, vedremo come l’impresa può scegliere l’allocazione ottima dei fattori produttivi (lavoro e capitale).
In particolare, l’impresa può applicare tre regole: la regola dell’isocosto più basso, la regola della tangenza, o la regola della spesa marginale.
Combinazione ottima dei fattori produttivi – breve premessa sui costi e sulla produzione
L’isoquanto di produzione
Come abbiamo visto nel post dedicato, la produzione nel lungo periodo viene rappresentata dall’isoquanto di produzione.
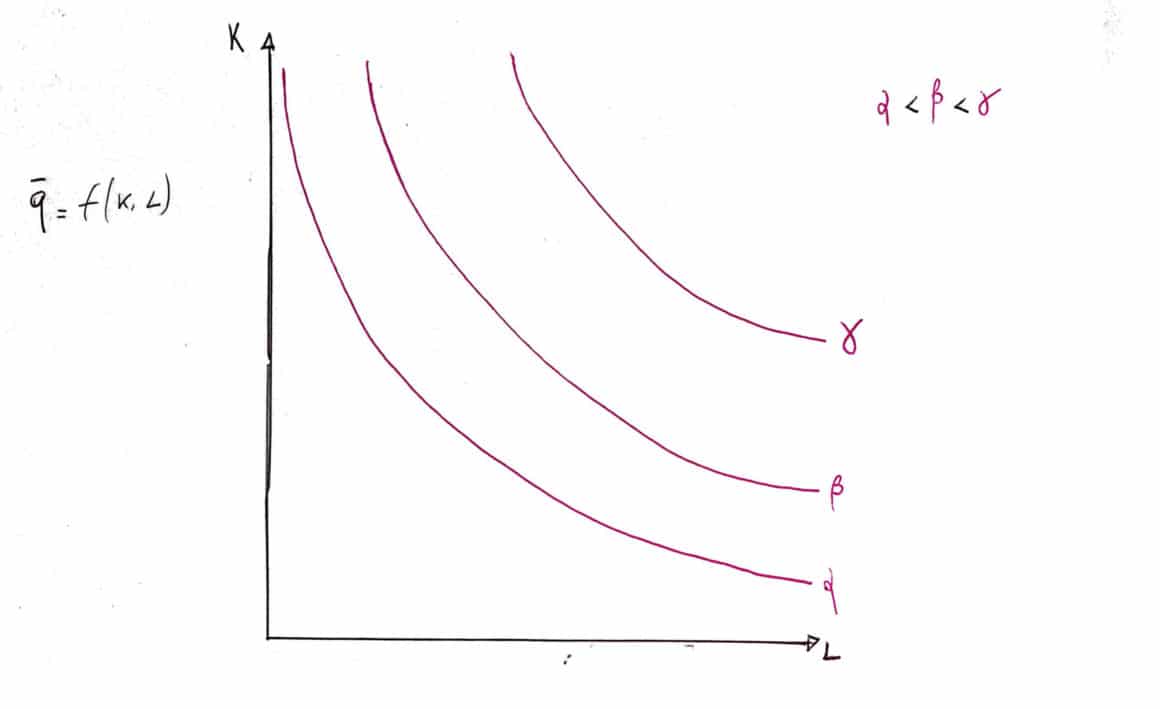
Ciascun isoquanto rappresenta una data quantità di output (q).
Lungo ogni isoquanto, la quantità di output è uguale (ciò che cambia è la combinazione dei due fattori produttivi (lavoro, L e capitale, K).
Gli isoquanti più distanti dall’origine rappresentano una maggiore quantità di output (q)rispetto a quelli più vicini all’origine.
La linea di isocosto
Come abbiamo visto nel post dedicato, i costi di lungo periodo vengono rappresentati dalla linea di isocosto.
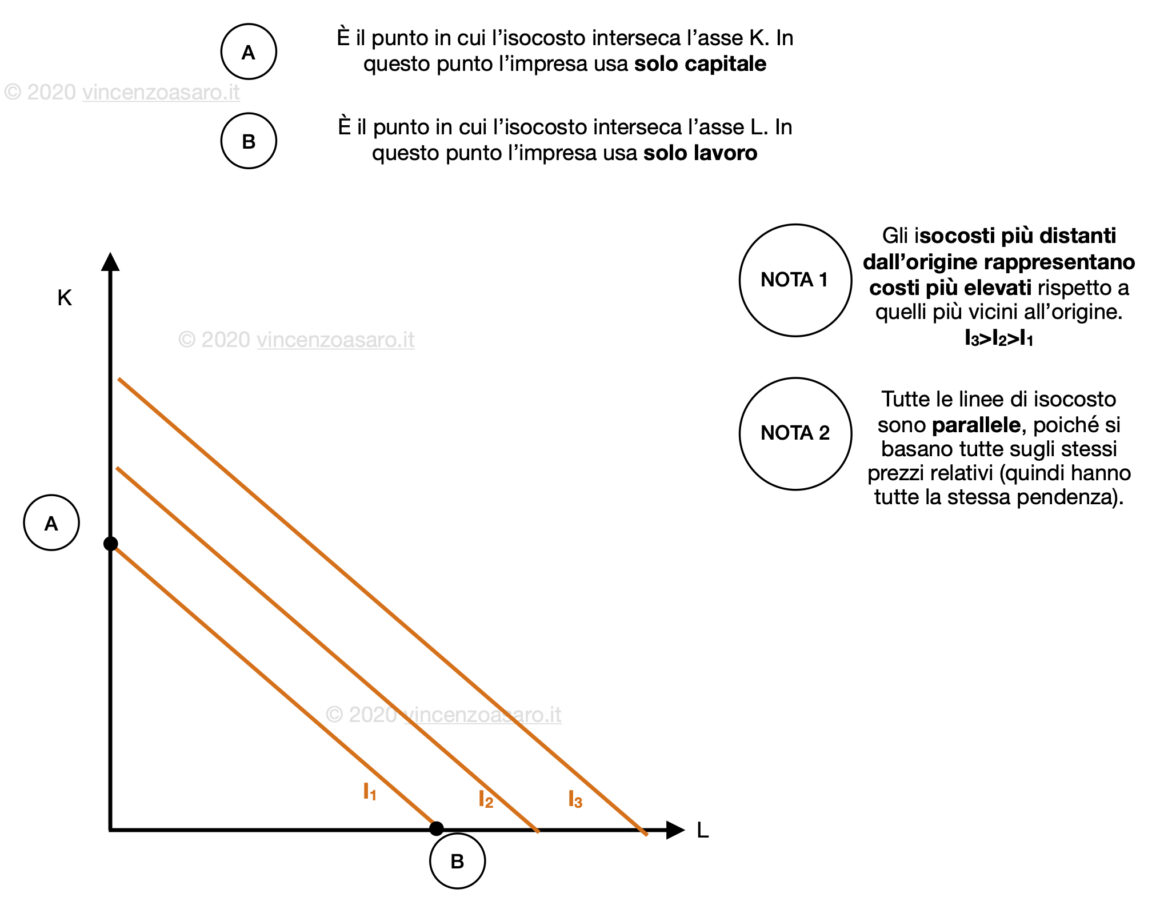
Ogni punto su una stessa linea di isocosto, rappresenta il medesimo costo (ciò che cambia è la combinazione di lavoro e capitale).
Anche in questo caso, le linee di isocosto più distanti dall’origine rappresentano un livello di costo maggiore.
Determinare la combinazione ottima dei fattori produttivi: combinare isoquanti e isocosti
Avendo le informazioni sui costi e sulla produzione, l’impresa deve scegliere come raggiungere un determinato livello di produzione minimizzando i costi.
Per farlo, può usare tre metodi:
- Regola dell’isocosto più basso
- Regola della tangenza
- Regola della spesa marginale
Vediamole brevemente una per una.
Regola dell’isocosto più basso
L’impresa produce la quantità che si trova sull’isocosto più basso (quindi che rappresenta un minore costo)tangente con l’isoquanto (che corrisponde al livello di produzione che l’impresa vuole raggiungere).
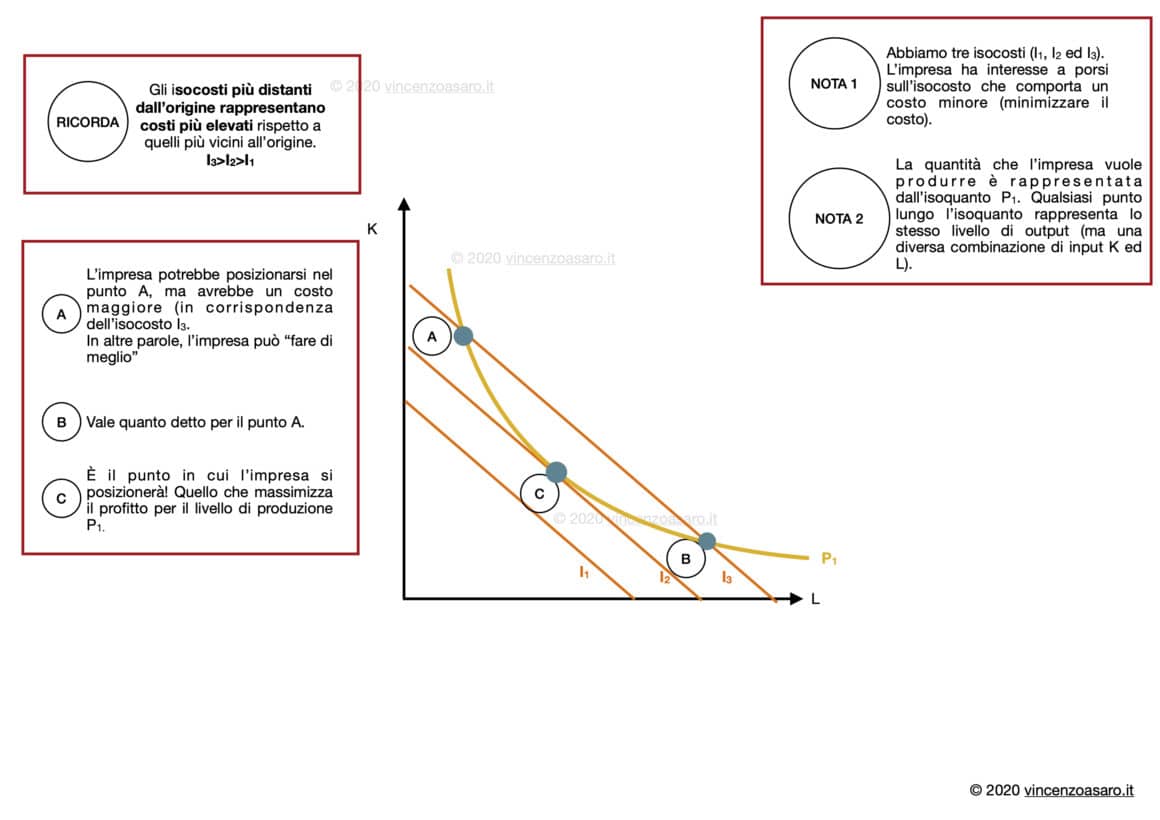
Ipotizziamo che un’impresa voglia produrre una data quantità di prodotto P1, rappresentata dall’isoquanto P1.
Dunque, l’impresa dovrà scegliere su quale punto dell’isoquanto P1 porsi, perché ogni punto comporta la quantità desiderata, ma con una combinazione diversa di lavoro e capitale.
Supponiamo che quest’impresa abbia le linee di isocosto I1, I2, I3.
Come possiamo vedere nei commenti contenuti nel grafico, l’impresa si posizionerà sul punto C.
Significa che il punto C rappresenta la combinazione ottimale di lavoro (L) e capitale (K)che permette all’impresa di produrre la quantità voluta (P1)minimizzando il costo (curva di isocosto I2).
Regola della tangenza
Come abbiamo visto nel post relativo alla produzione, la pendenza dell’isoquanto è rappresentata dal Tasso Marginale di Sostituzione Tecnica: MRTS (Marginal Rate of Technical Substitution).
Mentre, nel post sui costi abbiamo visto che la pendenza dell’isocosto è data da w/r.
Dove w è il costo orario del lavoro, e r è il costo orario del capitale.
*Ricorda che, quando abbiamo calcolato la retta di isocosto, nel post sui costi, abbiamo detto che:
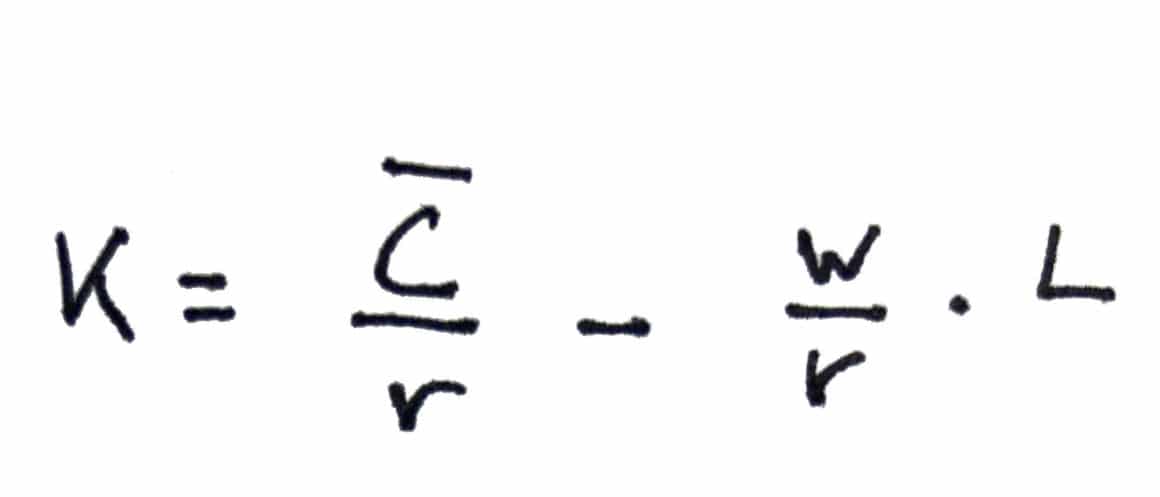
Dunque, per trovare con strumenti matematici il punto C del grafico precedente, dobbiamo semplicemente uguagliare le due pendenze.
Quando le pendenze sono uguali, troviamo il punto di tangenza, e quindi il punto C!
Il punto di tangenza è quello in cui le due pendenze si eguagliano:
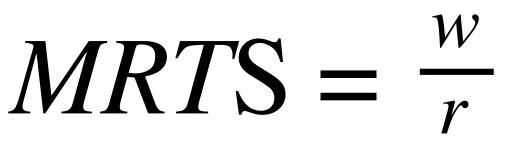
Ma sappiamo che
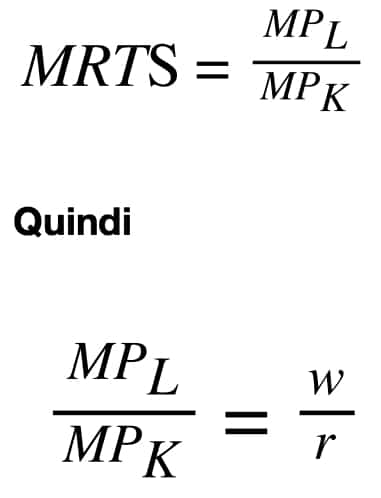
Quest’ultima equazione ci fa capire che il punto di ottimo si ha quando il rapporto tra la produttività marginale del lavoro e la produttività marginale del capitale [primo membro]è uguale al rapporto tra il costo unitario del lavoro (w)e il costo unitario del capitale (r).
Questo ci porta alla terza modalità per determinare il punto di efficienza dell’impresa.
Regola della spesa marginale
Il terzo punto è molto intuitivo. È sostanzialmente un modo diverso di scrivere l’ultima equazione che abbiamo visto.
La scelta ottima dell’impresa si può avere anche quando:
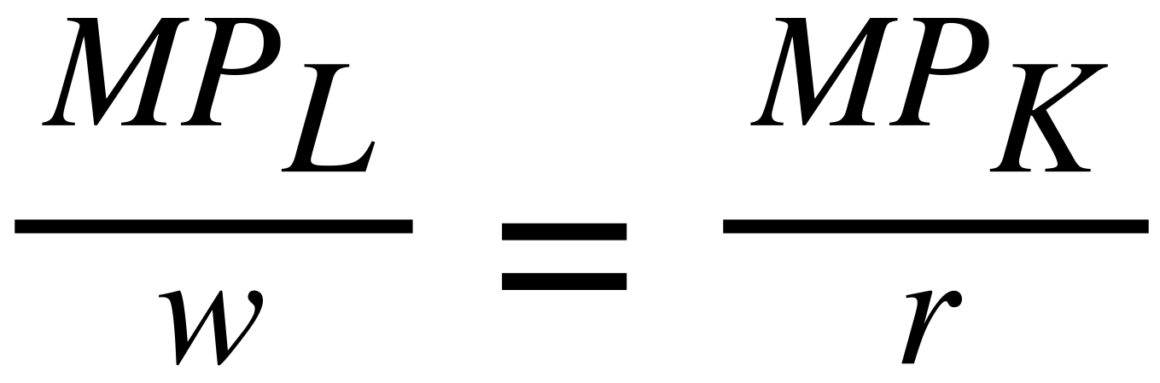
Il prodotto marginale del lavoro diviso il suo costo unitario è uguale al prodotto marginale del capitale diviso il suo costo unitario.
Esercizio svolto sulla combinazione ottima dei fattori produttivi
Un esercizio svolto sul determinare la combinazione ottima dei fattori produttivi ci aiuterà a chiarirci le idee.
Ipotizziamo che un’azienda abbia la seguente funzione di produzione:
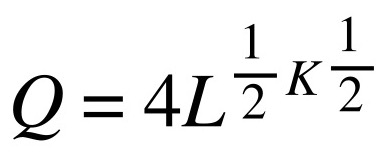
Il costo unitario del fattore lavoro è di 40 €, quindi w = 40.
Il costo unitario di utilizzo del capitale è 10 €, quindi k = 10.
Vogliamo usare la regola della tangenza, dunque per calcolare il tasso marginale di sostituzione tecnica (MRTS), ci serve il prodotto marginale del lavoro (MPL)e il prodotto marginale del capitale (MPK).
Calcoliamo il prodotto marginale del lavoro (MPL)
Come sappiamo, per calcolare MPL, dobbiamo derivare la funzione per L.
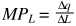
Svolgiamo i calcoli. Se qualcosa nei calcoli non dovesse essere chiaro, potete rivedere le regole di derivazione della radice.
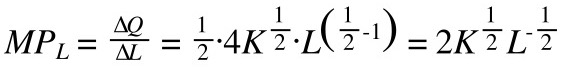
Calcoliamo il prodotto marginale del capitale (MPK)
Per calcolare MPK, dobbiamo derivare la funzione per K.
Di seguito trovate i calcoli svolti, ma se qualcosa non dovesse essere chiaro, anche in questo caso potete rivedere le regole di derivazione della radice.
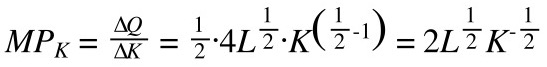
Determiniamo la combinazione ottima dei fattori produttivi
Adesso abbiamo tutto ciò che ci occorre per determinare la combinazione ottima dei fattori produttivi. Conosciamo il prodotto marginale del lavoro (MPL), il prodotto marginale del capitale (MPK), il costo unitario del fattore lavoro (w)e il costo unitario del fattore capitale (r).
Come abbiamo visto, la condizione di ottimizzazione (regola della tangenza)è:
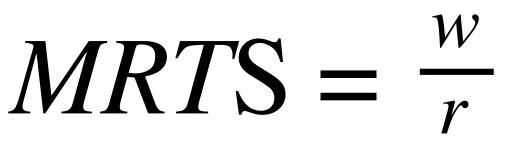
Sappiamo che:

Calcoliamo il nostro MRTS, sostituendo il prodotto marginale del lavoro e del capitale che abbiamo trovato:
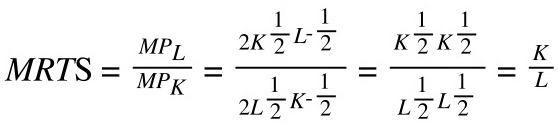
Ricordiamo che MRTS è la pendenza dell’isoquanto di produzione. Calcolandolo, abbiamo visto che per questa funzione di produzione, abbiamo:
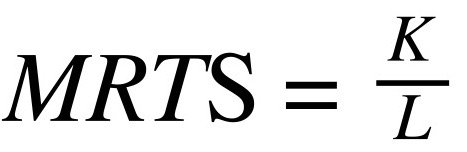
Abbiamo calcolato il nostro MRTS.
Ora non ci resta che imporre la condizione di tangenza, che ricordiamo essere:
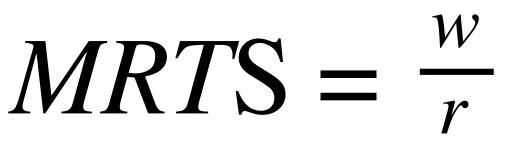
Al primo membro, abbiamo MRTS appena calcolato. Al secondo membro abbiamo w/r, ma sappiamo che w=40, e r=10, quindi:
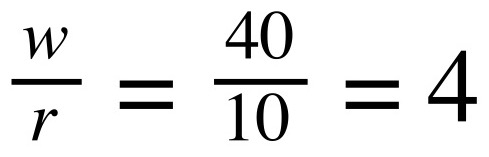
Abbiamo calcolato tutto l’occorrente. Adesso verifichiamo la condizione di tangenza:
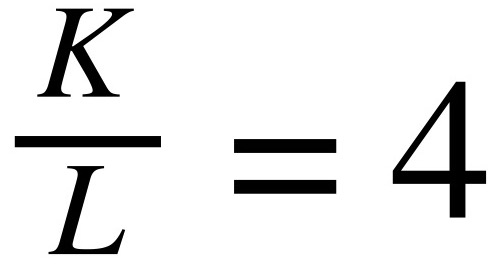
Abbiamo ottenuto che la combinazione ottima dei fattori produttivi è di impiegare 4 unità di capitale per ciascun lavoratore.
Questo esempio conclude la discussione sul modo in cui l’impresa scelga la combinazione ottima dei fattori produttivi.
Se sei arrivato a leggere fino a qui, lascia pure un commento!


Sono uno studente lavoratore ed avevo iniziato a studiare sulle dispense della Prof di Microeconomia. Le ho trovate confuse e fin troppo semplificate. Stesso vale per le esercitazioni che omettevano quasi tutti i passaggi e le formule. Ero sfiduciato. Grazie a questo blog ho capito ed assimilato facilmente diversi concetti che prima non mi erano chiari, inclusi grafici ed esercizi. Ho rielaborato il tutto in un mio scritto ed in circa un mese e mezzo (lavorando), ho portato a casa un bel 26!!!! GRAZIE DAVVERO!!! Vado ora di Politica economica…. Meno 2 al traguardo!!!!
Sono felice di averti potuto dare una mano, Alessandro!